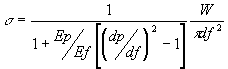
Bend Radius. Other than permanent damage due to extreme ionizing radiation, fiber failure is caused by crack growth which extends through the glass causing it to break. Tensile loading during cable installation and static bending induced stress contribute to fiber aging by inducing and growing cracks. These stresses are most often the focus of studies which look at long term reliability. The test assumes that long lengths of fiber are used, as in the telecommunication industry, and that a derated tensile strength, which provides a safety margin, can be calculated based on the proof strength. In other words, s_max must be some fraction of the actual proof strength or

s_max = s _f / f

where s_max is the maximum amount of tensile stress that the fiber can withstand safely during use, s_f is the proof strength of the fiber, and f is the safety coefficient.

A typical safety coefficient is f = 5. Uncoated optical fiber has a stress limit of 500 kg/mm² or 700 kpsi (where the conversion is 1 kg/mm² = 1.422 kpsi). Advertised proof strengths for coated space grade multimode fiber are in the 100 to 200 kpsi range. The relationship between tensile load and tensile strength for an optical fiber is

s_f = W/p d_f²

where d_f is the fiber outer diameter, W is the tension load value applied to determine the tensile stress. The expression for determining tensile stress for coated optical fiber is

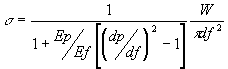
where: E_p = Young's modulus of the coating, E_f = Young's modulus of the fiber, d_p = coating outer diameter, d_f is fiber outer diameter[9]

Notice that the second term is the expression for tensile stress of an uncoated optical fiber. Therefore, the relationship between the tensile strength of a coated fiber and an uncoated fiber can be expressed as s =As _f where A is the expression

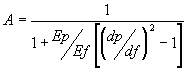
The value for A will then describe by how much a given coating system can reduce the tensile stress induced upon the fiber optic strand given a constant load W. If we assume that the value of E_p= 200 kg/mm², E_f = 7100 kg/mm², an outer diameter for fiber d_f =140 microns, and an outer diameter d_p for the coating of 250 microns, then the tensile strength is s =0.94s _f . In other words, the coated fiber system is 6% stronger than bare fiber. This value can be increased by increasing the values of d_p, the outer diameter of the coating, and/or by increasing the Young's modulus, which implies use of another type of material with a larger E_p. For example, with the same E_p used above, increasing the outer diameter to 500 microns will increase the strength of the coated fiber by 25%. Using the same diameter value as above and increasing E_p to 300 kg/mm² will improve the tensile strength by 33%. Note that UV curable, soft, acrylates have an E_p in the range of 0.1 to 0.3 kg/mm² and UV curable hard acrylates have an E_p in the range 50 to 100 kg/mm². In most acrylate coated fibers, two coating layers of are used to increase both the outer diameter and the modulus.

If s is the rupture strength of the coated fiber optic strand and a safety coefficient of 5 is used, then the safe-stress must be less than 0.2s, or s_max< 0.2s. Based on the results found previously we can express the relationships between the minimum bend radius of the coated fiber and the outer diameter of the fiber coating which optimizes long term reliability. By increasing the outer diameter of the coating it was shown that the strength of the fiber increases. That being so, the minimum allowable stress s_max can be related to long term bend radius by s_bend = E_f d_f / 2 R, where R is the bend radius and E_f & d_f are defined above. If the limit on bending stress is that it be equal to the safe stress value s_max then the equation can be rewritten as R = E_f d_f / 2 s_max . As the safe stress increases with a larger diameter coating and/or by a coating material that increases Young's modulus, the safe minimum bend radius decreases.

---

Table of Contents

Next Section: Summary and Definitions